

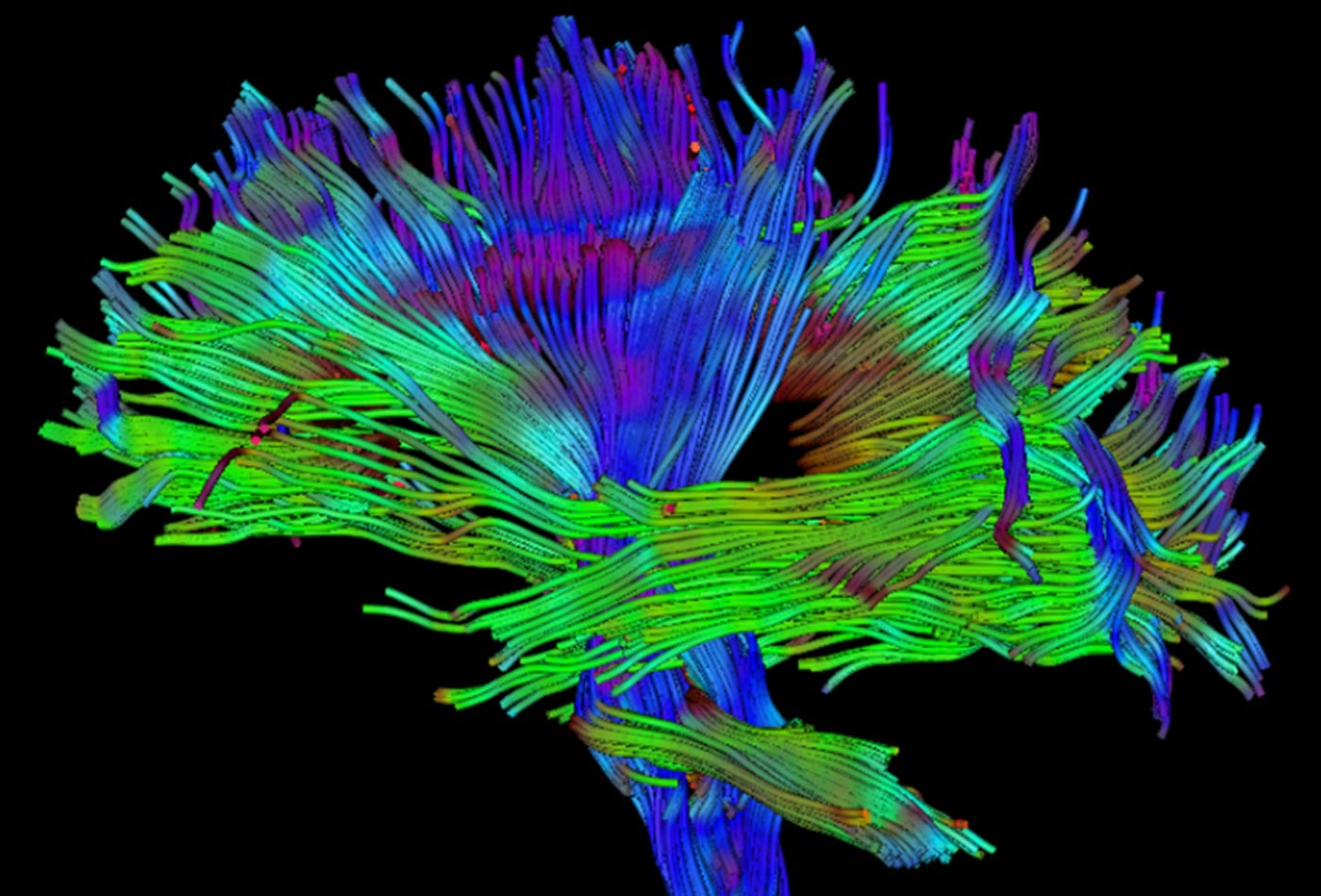
The simplest approach to DW-MRI registration consists in registering these datasets using a single transformation obtained from a representative volume, such as the Fractional Anisotropy (FA) ( Pierpaoli and Basser, 1996), or the non-diffusion-weighted (b0) image. However, registration of such data is more challenging than for three-dimensional scalar images, not only because of its high dimensionality (hundreds of volumes) or noise and artifacts present in MR scans ( Jones et al., 1999 Behrens et al., 2003 Le Bihan et al., 2006 Stobbe and Beaulieu, 2011), but because the signal, and any subsequently estimated local fiber orientation model, must remain consistent with the underlying fiber geometry after image transformations ( Zhang et al., 2006 Barmpoutis et al., 2007 Cheng et al., 2009 Dhollander et al., 2010 Verma and Bloy, 2010 Yap et al., 2010 Du et al., 2011 Geng et al., 2011 Raffelt et al., 2011). Registration of DW-MRIs is a key step in population studies or brain atlases construction, among other important tasks. This information can be used to estimate the local orientation of fiber bundles, since water diffusion is favored along the fiber orientation, providing critical information for neuroscience and clinical studies ( Jones et al., 1999 Basser and Jones, 2002 Filler, 2009). In particular, we show that AI improves the registration accuracy in many cases over existing state-of-the-art algorithms, while providing registered raw DW-MRI data, which can be used for any subsequent analysis.ĭiffusion-weighted magnetic resonance imaging (DW-MRI) is a non-invasive imaging technique that measures the diffusion of water molecules in biological tissues, such as the brain’s white matter, along several gradient directions.
We demonstrate that AI registration of DW-MRIs is a powerful alternative to volume and tensor-based approaches.
#Medinria dti software
Moreover, we generalize the concept of angular interpolation (AI) to non-linear image registration, and implement it in the FMRIB Software Library (FSL). In this work, we first extensively compare the performance of registration algorithms based on (i) angular interpolation, (ii) non-diffusion-weighted scalar volume (b0), and (iii) diffusion tensor image (DTI). A new algorithm based on angular interpolation of the diffusion-weighted volumes was proposed for affine registration, and does not rely on any specific local diffusion model. ODF-based approaches are more recent and computationally challenging, but also better describe complex fiber configurations thereby potentially improving the accuracy of DW-MRI registration. Tensor-based registration methods rely on a model that does not completely capture the information contained in DW-MRIs, and largely depends on the accurate estimation of tensors. Models such as the diffusion tensor or orientation distribution function (ODF) have been used for this purpose. Alternatively, model-based registration algorithms have been proposed to exploit information on the preferred fiber orientation(s) at each voxel. Given the high dimensionality of the data, registration is usually performed by relying on scalar representative images, such as the fractional anisotropy (FA) and non-diffusion-weighted (b0) images, thereby ignoring much of the directional information conveyed by DW-MR datasets itself. Registration of diffusion-weighted magnetic resonance images (DW-MRIs) is a key step for population studies, or construction of brain atlases, among other important tasks.


 0 kommentar(er)
0 kommentar(er)
